Erklärungen in Mathematik, Physik und Physikalischer Chemie

I) - Das gaußsche Wellenpaket: Herleitung und Betrachtung (zu: Mathematik, Physik)	(18 Seiten)
Die mathematische Konstruktion des gaußschen Wellenpakets durch harmonische Wellen und sein zeitlicher Verlauf. mehr ...
C) - Herleitung einer Funktionaldeterminante (zu: Mathematik, Physikalische Chemie)	(19 Seiten)
Schritt-für-Schritt-Erklärung, wie man auf die Struktur einer Funktionaldetermiante kommt. mehr ...
D) - Grundzüge der Wahrscheinlichkeitsrechnung - einfach erklärt (zu: Mathematik)	(28 Seiten)
Eine Einführung in die Wahrscheinlichkeitsrechnung, u.a. in Zufallsexperimente, in die Gesetze der Wahrscheinlichkeit und in ihre grundlegenden Begriffe. mehr ...
G) - Prägnantes Beispiel einer Koordinatentransformation (zu: Mathematik) mehr ...	(3 Seiten)
B) - Der Punkt: nach Euklid und anschaulich (zu: Mathematik, Physik) mehr ...	(4 Seiten)
H) - Superposition und Interferenz von Wellen (zu: Physik)	(21 Seiten)
Vom Sinn komplexer Wellen zu Wellen am Spalt/Doppelspalt bis hin zu stehenden Wellen und Schwebungen. mehr ...
Je weiter oben sich ein Artikel in der Liste befindet, desto häufiger ist er in der Vergangenheit angeklickt worden, die alphabetische Nummerierung gibt an, in welcher Reihenfolge die Artikel zeitlich entstanden sind, und rote Buchstaben bedeuten, dass diese aufeinander aufbauen, so A) und C), A) und B) oder A) , H) und I).

- Literaturverzeichnis	(1 Seite)
- Glossar; Unglückliche, naturwissenschaftliche Ausdrücke; Liste der verwendeten Symbole; Postulate der Quantenmechanik	(8 Seiten)

Zum Lesen der Texte benötigen Sie den Acrobat Reader, den Sie hier kostenlos herunterladen können.

Kurzartikel B: Der Punkt: nach Euklid und anschaulich (4 Seiten)

Welche Ausdehnung hat ein Punkt und wie müsste man ihn definieren, damit man ihn in jedem Raumbereich auch zeichnen kann? Hier werden zwei unterschiedlich existierende Punktvorstellungen diskutiert und dazu Beispiele aus Mathematik und Physik genannt. So werden Koordinatenpunkte, Punkte aus der Physik mit einer Ausdehnung und die Punktmassen, ebenfalls ein Begriff aus der Physik, behandelt.

Verwendete Begriffe und Namen: Euklid, Koordinatenpunkt, Massenpunkt, Punkt, anschaulicher und euklidischer bzw. mathematischer Punktbegriff, Punktmasse.

	Artikel C: Herleitung einer Funktionaldeterminante (19 Seiten)
	Hat man ein Integral		vorliegen und möchte dieses
	in ein System mit ebenen Polarkoordinaten transformieren, so wird in diesem Artikel Schritt für Schritt erklärt, wie man auf den Ausdruck

der zugehörigen Funktionaldetermiante (= Jacobi-Determinante) kommt, durch den sich das		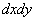ersetzen lässt (s. die Abbildung). Mit
dem so entwickelten Schema wird analog eine Funktionaldeterminante im 3-dimensionalen Raum für beliebige krummlinige Koordinaten-

systeme verständlich, so z.B. für eine Transformation des Differentialausdrucks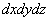

in die sphärischen Polarkoordinaten

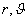und

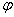.	Schließlich kann damit sogar nachvollzogen werden, wie man allgemein den Ausdruck einer Funktionaldeterminante in Form einer

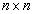	Determinante erhält.
[Dieser Artikel ist geschrieben worden, um in der Quantenmechanik den Einsatz der Funktionaldeterminante zu verstehen. Die Umwandlung des Differentialausdrucks eines beliebigen krummlinigen Koordinatensystems in den Differentialausdruck eines anderen beliebigen krummlinigen Koordiantensystems wird in dieser Ausführung nicht erörtert.]

Verwendete Begriffe: Determinante, partielles Differential, Funktionaldeterminante, Jacobi-Determinante, kartesische Koordinaten, Kugelkoordinaten, ebene Polarkoordianten, sphärische Polarkoordinaten, Raumwinkel.

*Inhalt* C.1 Überblick C.2 Transformationen mit zwei Veränderlichen C.3 Der Grenzzustand von Flächenelementen C.4 Zur Größe der Fläche von differentiellen Flächenelementen C.5 Umschreibung eines differentiellen Flächenelements durch kartesische Koordinaten C.6 Die Funktionaldeterminante C.7 Übertragung auf sphärische Polarkoordinaten C.8 Zu unendlich kleinen Flächenelementen C.9 Zusammenfassung C.10 Aufgaben C.11 Literatur

	Artikel D: Grundzüge der Wahrscheinlichkeitsrechnung - einfach erklärt (28 Seiten)

	Dieser Artikel gibt einen ersten Einblick in die Grundlagen der Wahrscheinlichkeitsrechnung. Dabei werden folgende Aspekte behandelt: Was hat es mit den zwei Gegenspielern Zufall und kausales Denken auf sich und was versteht unter dem mathematischen Zufall? Was ist ein Zufallsexperiment und welche relevanten Begriffe gibt es hierzu? Wie berechnet man die Wahrscheinlichkeit eines zufälligen Ereignisses und wovon handelt das empirische Gesetz der großen Zahl? (Einige leichte Gesetzmäßigkeiten aus der

Wahrscheinlichkeitsrechnung werden dazu zusammengestellt.)
Weiter aber auch: Welche 2 Arten von Zufall gibt es und welche 3 Bedeutungen lassen sich mit dem Wort Wahrscheinlichkeit verbinden?
Ferner: Worum geht es bei mehrstufigen Zufallsexperimenten? Zur Darstellungsweise über ein Baumdiagramm siehe dazu die Abbildung.
Außerdem werden die Größen Zufallsvariable, Erwartungswert, Varianz und Standardabweichung erläutert.

Verwendete Begriffe und Namen: Ausfall, Ausgang, Demokrit, Elementarereignis, Ereignis, Ereignisraum, Ergebnismenge, Ergebnisraum, Erwartungswert, absolute und relative Häufigkeit, Realisation, Standardabweichung, Varianz, Wahrscheinlichkeit, Wahrscheinlichkeitsverteilung, Zufall, Zufallsexperiment, Zufallsgröße, Zufallsvariable.

*Inhalt* D.1 Überblick D.2 Zufall und Notwendigkeit D.3 Begriffe zu Zufallsexperimenten D.4 Wahrscheinlichkeit von Ereignissen D.5 Zufall und Wahrscheinlichkeit im Alltag D.6 Mehrstufige Zufallsexperimente D.7 Die Zufallsvariable D.8 Der Erwartungswert D.9 Varianz und Standardabweichung D.10 Zusammenfassung D.11 Aufgaben D.12 Literatur

Kurzartikel G: Prägnantes Beispiel einer Koordinaten-transformation (3 Seiten)

Hier wird exemplarisch ein sehr einfaches und prägnantes Beispiel einer Koordinatentransformation vorgestellt und ausgeführt, aus welchen drei Teilen jede Koordinatentransformation besteht. Des Weiteren wird an diesem Beispiel demonstriert, wie beide Koordinatendarstellungen (vor und nach der Transformation) das gleiche Rechenergebnis ergeben.

Verwendete Begriffe: Definitonsbereich, Differentialausdruck, Einheitskreis, Integrationsgrenzen, Koordinatentransformation.

	Artikel H: Superposition und Interferenz von Wellen (21 Seiten)

	Wellen sind ein zentrales Phänomen in der Physik. Nicht nur beim Schall und beim Licht, sondern auch bei der Untersuchung von Atomen sind vielfach Wellenerscheinungen anzutreffen. In welchen vielfältigen Formen sich diese überlagern können, wird hier an einigen typischen Beispielen dargestellt. Nach einer kurzen Einführung über Wellen wird die komplexe Erweiterung des Wellenbildes und ihr Sinn herausgestellt. Anschließend folgen Überlagerungen von Wellen im Allgemeinen und hinter Spalten und Doppelspalten, für das das Modell der Teilbündel physikalisch mittels huygenscher Elementarwellen begründet und hergeleitet wird (s. die Abbildung). Zum Schluss werden stehende Wellen und Schwebungen behandelt. Die hier besprochenen Wellen und Wellengebilde werden z. T. auf ihre Verträglichkeit mit der allgemeinen Wellengleichung überprüft.

Verwendete Begriffe: Huygensche Elementarwelle, Interferenz, Schwebung, Spalt bzw. Doppelspalt, Strahlen, Superposition, Superpositionsprinzip, Teilbündel, harmonische Welle, stehende Welle, Wellenbündel, allgemeine Wellengleichung, Wellengruppe.

*Inhalt* H.1 Überblick H.2 Einführung in die Wellenlehre H.3 Wellen mit komplexem Anteil H.4 Überlagerung von Wellen H.5 Wellen am Spalt/Doppelspalt H.6 Stehende Wellen H.7 Schwebungen H.8 Lösungen der allgemeinen Wellengleichung H.9 Aufgaben

	Artikel I: Das gaußsche Wellenpaket: Herleitung und Betrachtung (18 Seiten)

	Kleine, lokale Größen spielen eine große Rolle im Verständnis des Mikrokosmos. So kann man Atome und Moleküle als lokalisierte Zustände auffassen, da sie nur in einem engen örtlichen Bereich existieren. Will man ganz allgemein physikalische Aussagen über solche Zustände erhalten, dann bedient man sich in der Physik (und hier speziell der Quantenmechanik) zunächst einmal des gaußschen Wellenpakets. So kann dieses für eine Ortsdarstellung von Teilchen im Mikrokosmos als auch für eine Impulsdarstellung solcher Teilchen formuliert werden. (Wenn daraufhin ein Darstellungswechsel zwischen den physikalischen Größen, wie z.B. vom Impuls- in den Ortsraum, vorgenommen wird, so gelangt man in der Quantenmechanik zu ganz fundamentalen Beziehungen, die für jede Berechnung nach ihr von großer Bedeutung sind.) In diesem Zusammenhang nehmen Betrachtungen über das gaußsche Wellenpaket eine Schlüsselstellung ein.

Was ein gaußsches Wellenpaket genau ist (s. auch die Abbildung) und wie es von harmonischen Wellen ausgehend konstruiert werden kann, ist das Thema dieses Artikels. Hierbei wird hauptsächlich der Fall behandelt, bei dem keine Dispersion vorliegt, man es also streng genommen mit Verhältnissen im Vakuum zu tun hat.
Jeder Schritt dieses Artikels wird parallel auf die Gültigkeit der allgemeinen Wellengleichung überprüft. Eine anschauliche Betrachtung des gaußschen Wellenpakets zu verschiedenen Zeiten und seines Trägers rundet den Artikel ab.

Verwendete Begriffe und Namen: Dispersion, Gauß, Modulation, gaußsche Verteilung, allgemeine Wellengleichung, Wellenpaket, gaußsches Wellenpaket.

*Inhalt* I.1 Überblick I.2 Herleitung eines Integralausdrucks aus der Überlagerung harmonischer Wellen I.3 Das gaußsche Wellenpaket I.4 Das gaußsche Wellenpaket zu verschiedenen Zeiten I.5 Eine anschauliche Betrachtung des Trägers I.6 Lösungen der allgemeinen Wellengleichung I.7 Zusammenfassung